Gabor^2
Approximating an image with Gabor functions.
Overview
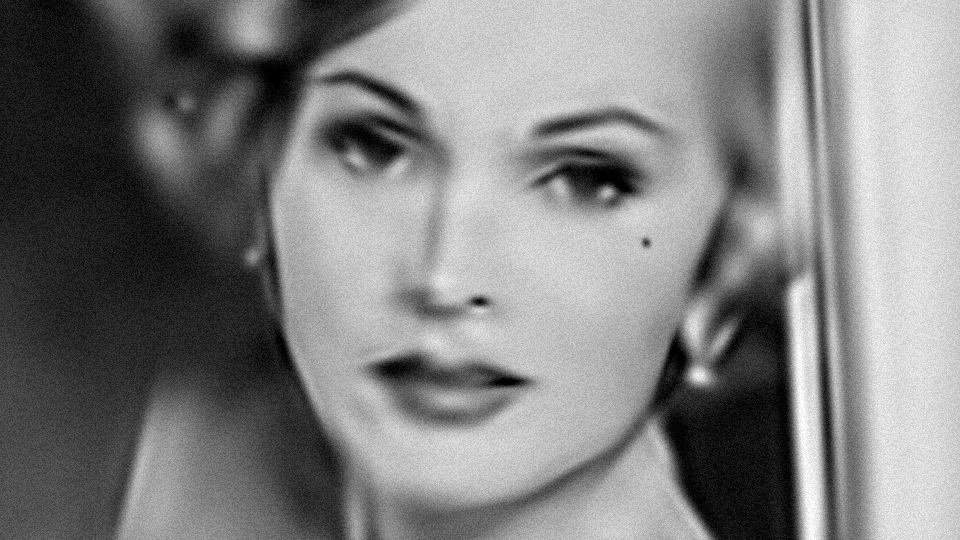
The above picture is a detail of a photo of Zsa Zsa Gabor reconstructed with 128 Gabor functions. You can see an interactive demo of the reconstruction in my Gabor^2 shader on Shadertoy. The code to generate this is up on my github.
Motivation
I made this after seeing some other impressive demonstrations of image compression/reconstruction on Shadertoy, including iq’s Audrey, Dave_Hoskins’ Sharbat Gula (warning: long load/compile time), and and’s Terminator (especially wow).
For a long time, I had wanted to see how Gabor functions could be used to reconstruct images, so I decided to give it a try. A single gabor function is encoded by eight parameters \(u\), \(v\), \(\rho\), \(\phi\), \(\ell\), \(s\), \(t\), and \(h\) defined by
\[g(x,y) = h \exp \left( -\frac{x'^2}{2 s^2} -\frac{y'^2}{2 t^2} \right) \cos \left( \frac{ 2 \pi }{ \ell} x' + \phi \right)\]where \(x' = (x - u) \cos \rho + (y - v) \sin \rho\) and \(y' = -(x - u) \sin \rho + (y - v) \cos \rho\).
The overall reconstructed image \(I(x,y)\) is a simple summation given by
\[I(x,y) = \sum_{i=1}^{n} g_i(x, y)\]with each \(g_i\) a separate Gabor model function. My original idea was to treat the problem as a gigantic nonlinear least squares problem and simultaneously solve for all of the Gabor function parameters to minimize the squared error between the original image and the reconstruction \(I(x,y)\). This turned out to be very slow, so instead I ended up with more of a greedy, one-model-at-a-time approach. I was especially interested in trying out Google’s Ceres solver for this project, but ended up avoiding it because it didn’t support constrained optimization.
Inequality constraints
Early on in my experiments, I ran into a problem: without constraints (or with just simple box constraints), the Gabor functions look pretty gross because they introduce a lot of high-frequency noise that sticks out like a sore thumb perceptually despite not spoiling the squared error too much (due to relatively low amplitude).
Compare the two images below:


Although the magnitude of the residual is roughly equal in each picture, the one on the left contains a number of Gabor functions whose Gaussian component spans multiple wavelengths of its sinusoidal component, giving Zsa Zsa a somewhat splotchy complexion. The one on the right enforces the constraint that \(\ell \geq 2 s\), that is, the wavelength of the sinusoid must be at least double the width of the Gaussian component. I also ended up enforcing inequality constraints on the shape of the Gaussian component as well. In terms of Gabor functions, we are restricting ourselves to a subset of functions that look more like brushstrokes, or short stacks of parallel long skinny Gaussians (up to about 2 or 3 wide).
Optimization method
Since ceres-solver doesn’t work well with inequality constraints (or at least didn’t at the time I began this project), I ended up looking at Manolis Lourakis’ levmar library. After a bit more experimentation it became clear that it would be prohibitively slow to fit all 1024 parameters at once (128 Gabor functions \(\times\) 8 parameters per model), so instead, a greedy approach was adopted.
In the greedy approach, a single model is generated at a time, at each iteration choosing the model which best minimizes the residual between the total reconstruction so far and the original image. Because the error landscape is highly non-convex, at each iteration, we randomly initialize 100 different models and perform LM fitting on the one which best minimizes the residual.
After all 128 models are chosen, optimization continues by randomly choosing a model to replace and then repeating the greedy single-model search to replace it.
As hinted in iq’s comments here, care should be taken to especially minimize the residual along the eyes, nose and mouth. Accordingly, my program allows the user to load a weight image which focuses where the error will be minimized. See the original input image on the left below, and the weight image (hastily doodled in Photoshop) on the right:

I let the program run on my 2013 MacBook Pro for a few days to produce the Gabor^2 image at the top of the article.
Source code
The image fitting program is now available on github. The repository also includes two small Python programs. The first was used to verify the analytical derivatives of the Gabor function for function fitting; the second is used to quantize and encode the Gabor function parameters into a compact representation suitable for use in a fragment shader.
Conclusion
Overall, I’m happy with how the project turned out. If I were going to put much more time in it, I would have looked at the following things:
-
faster optimization with GPU
-
try to get full optimization (as opposed to greedy, incremental method) working
-
generate color images
-
find lighter-weight dependencies for matrices, image loading, and display than OpenCV (perhaps eigen3, stb_image, and imgui?)
If anyone knows of a tiny library that integrates easily with C/C++ and elegantly handles image loading and display, I’m happy to hear about it!
Comments
You can use farbfeld for images: it's on suckless.org. Insanely simple, very useful.
Thanks, will check it out!
Comments are closed, see here for details.