Flow Free solver

Fast automated solver for Flow Free puzzles written in C.

GIF of the final program in action (see below if you’re unfamiliar with Flow Free):

Standard admonishments apply: feel free to skip ahead to the end; also, don’t hesitate to try out the code, which is up on github as always.

Overview

I like puzzles. Well, more precisely, I enjoy problem solving, and puzzles present nice, neat, self-contained problems to solve from time to time. But one thing I like even better than solving a puzzle is writing programs to automatically solve a whole lot of puzzles, fast.

Here’s a couple of screenshots from the mobile game Flow Free, in case you’re unfamiliar:

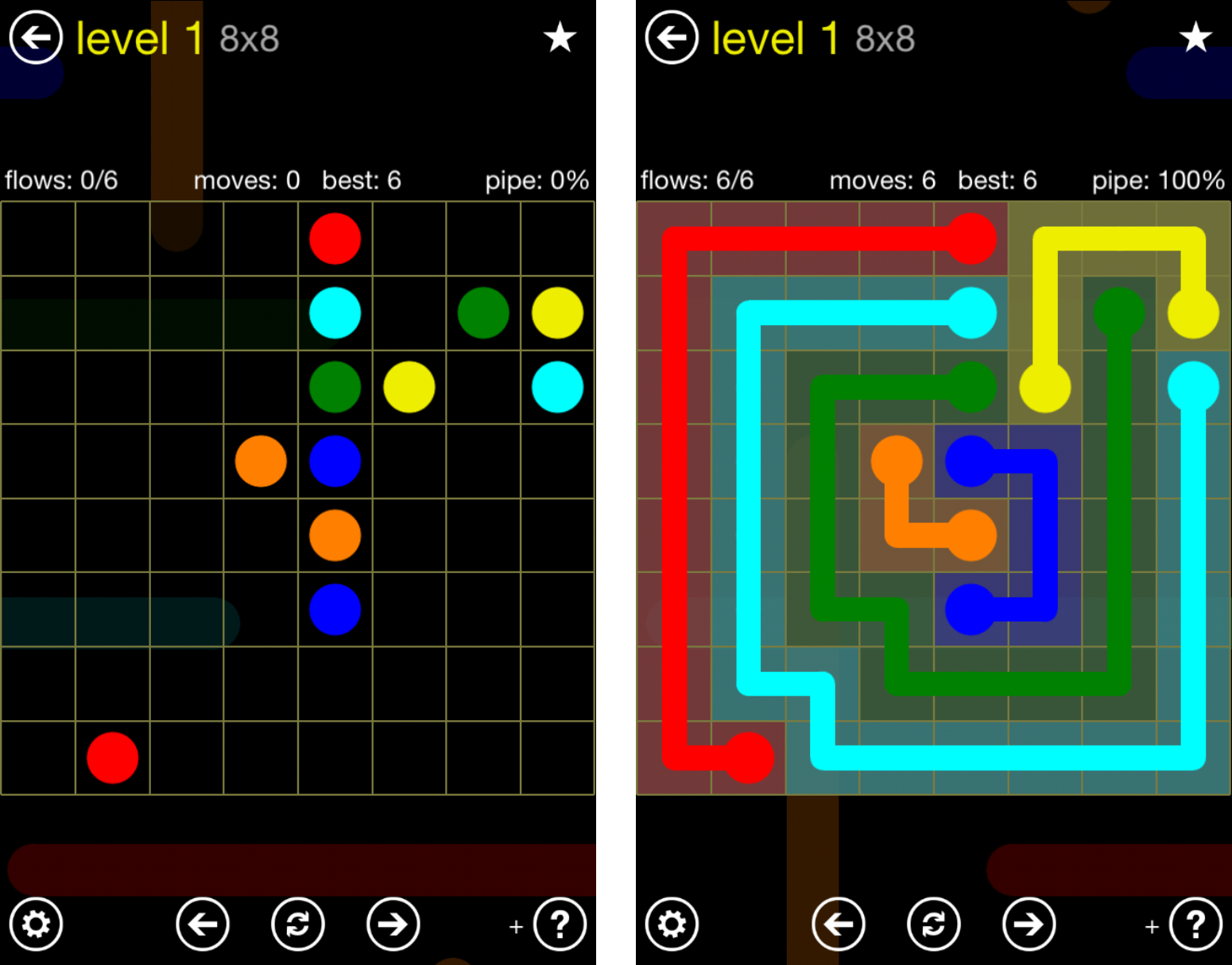
The game takes place on a grid which starts out empty, except for a number of pairs of colored dots (as shown on the left). The objective is to draw paths or flows such that all pairs are connected and all of the empty cells are filled (as shown on the right). Puzzles range from 5x5 all the way up to 14x14, and they may have anywhere from 5 to 16 colors of flows.

I’ve had Flow Free on my iPhone for years, and it’s saved me from boredom on many a subway or airplane. From time to time I’ve wondered how hard it would be to write a good automated solver for it, but I never took on the project until this summer, when I found myself with a few dozen hours of flights on which to occupy myself.

I developed the bulk of my solver over about a week of travel through Indonesia, Singapore, and Malaysia; when I got back home, I added about an order of magnitude’s worth of speed optimizations and some ANSI cursor commands to produce animated solutions like the one shown above. The program also outputs SVG images, which became the basis for many of the figures in this post.

By the way, I did dig up some prior work on the subject, but I only started looking for it once I had finished my solver. If you’re curious, there’s a list of related efforts at the very end of this post. As far as I can tell, my solver is the only one I’m aware of that can tackle large puzzles (e.g. 12x12 and up) in a reasonable amount of time.

Framing the problem

From an AI perspective, there are at least two substantially different ways to frame the Flow Free puzzle: the first is as a constraint satisfaction problem (CSP), and the second is as a shortest path problem. The former is the domain of SAT solvers and Knuth’s DLX, whereas the latter is the domain of Dijkstra’s algorithm and A* search.

At first blush, considering Flow Free as a CSP seems like a simpler formulation, because the constraints are so simple to state:

• Each free space must be filled in by a color.
• Each filled-in cell must be adjacent to exactly two cells of the same color.
• Each dot must be adjacent to exactly one filled-in cell of the same color.

In contrast, shortest path algorithms like Dijkstra’s and A* seem ill-suited for this problem because the zig-zaggy flows found in puzzle solutions rarely resemble short, direct paths:

Despite this apparently poor fit, I decided to take the “A*-like” approach for two main reasons:

1. I spent years in grad school coding up search-based planners with A*.
2. When you have a hammer, the whole world looks like a nail.

Searching puzzle trees

Although finding shortest paths is a general graph search problem, my solver operates on a tree rooted at the initial puzzle state. Each node in the tree not only stores a puzzle state, but also the current position of each flow. We can generate a successor for a state – i.e. its “child” in the tree – by extending one of the flows into an empty cell adjacent to its current position.

It’s vitally important to reduce the branching factor – the average number of children per node – as much as possible, because a larger branching factor means searching exponentially more nodes. For example, a tree of branching factor 2 fully built out to depth of 10 has a modest 1,023 nodes, but doubling the branching factor to 4 would increase the tree size to 349,525!

So to keep our branching factor small, for any state we will designate a single active color which is permitted to move. Say we are solving a puzzle with 6 colors. If we allow moves from any flow’s current position, a node might have as many as 24 children (6 colors times 4 directions of motion per color); however, imposing an active color reduces the maximum number of children to 4.

Which color should we choose to be active? Probably the most constrained one – that is, the color with the fewest possible moves. For example, consider the puzzle below, with the colored cell backgrounds indicating the initial position for each flow. Both blue and cyan have only one valid move available, but green has four:

Hence, we should choose blue or cyan as the active color now, and postpone moving green until later, in hopes that the board has gotten more crowded by then. In the board above, we would say that the cyan and blue flows have forced moves because there is only a single free space next to the current position of each one.

Restricting moves to a deterministically-chosen active color has another important side benefit: it prevents duplicate states from arising in the tree. Otherwise, we could imagine arriving at the same state via two different “routes” which differ only in the order the flows are created (say moving red-then-green vs. moving green-then-red).

Heuristic search

Although we could use breadth-first search to solve the puzzle, I found that it’s significantly faster to go with best-first search instead. The method I ended up using is kind of a poor man’s A* search in that it computes two quantities for each state \(x\):

• a cost-to-come \(g(x)\) that considers all of the moves made to get to this state; and
• a cost-to-go estimate \(h(x)\) that estimates the remaining “distance” to a goal state.

My program defines the cost-to-come \(g(x)\) by counting up the “action cost” of each move. Each move incurs one unit of cost, with two zero-cost exceptions: completing a flow, and forced moves.

The heuristic cost-to-go \(h(x)\) is simply the number of empty spaces remaining to be filled. In terms of A* search, this is an inadmissible heuristic for my cost function because it disregards the possibility of future zero-cost moves; nevertheless, it works pretty well in practice.

For best-first search, I put the nodes in a heap-based priority queue which is keyed on the total cost \(f(x) = g(x) + h(x)\) for each node \(x\). As new moves are generated, they are placed onto the queue; the next one to be dequeued will always be the one with the minimum \(f(x)\) value.

As a concrete illustration, consider the tiny puzzle below:

Red has made two moves, but the first was forced, so the total cost-to-come \(g(x)\) is 1. There are 8 empty squares remaining, so the cost-to-go \(h(x)\) is 8. Hence we see the total cost \(f(x) = 8 + 1 = 9\).

Other forced moves

Consider this puzzle state:

Given the moves made by blue, the only way that the free space to the right of the orange flow could get occupied is if orange moves into it. From this example, we can now say a move is forced:

• …if a flow has only one possible free cell to move into (the original definition); or,

• …if an empty space is adjacent to a single flow’s current position, and it has only one free neighbor.

Recognizing the second situation is a bit more code-intensive than the first, but it’s worth it, because we are always looking for ways to reduce the branching factor. Without considering this type of forced move, it might seem like orange has three possible moves, but two of them are guaranteed to result in an awkwardly leftover empty square.

Dead-end checks

Sometimes, advancing a flow may leave behind a square that has a way into it, but no way out – for instance, the one marked with an “X” below:

After any move – e.g. completing the red flow above – we can recognize nearby “dead-end” cells by looking for a free cell that is surrounded by three completed path segments or walls (the current position or goal position of an in-progress flow don’t count). Any state containing such a dead-end is unsolvable, and we need not continue searching any of its successors.

Detecting unsolvable states early can prevent a lot of unnecessary work. The search might still eventually find a solution if we didn’t recognize and discard these, it might just take a lot more time and memory, exploring all possible successors of an unsolvable state.

Stranded colors and stranded regions

It’s possible that extending one flow can totally block off another one, preventing its completion. This can be as simple as surrounding a flow’s current position so it has nowhere to go, like the poor yellow flow in this state:

In a more subtle case, one flow can divide up the free space so that it is impossible to connect another flow’s current position to its eventual goal, like blue depriving red in the image below:

Finally, a move may create a bubble of freespace that is impossible to fill later, like the top-left 4x2 free area here:

Although red, cyan, and orange can all enter the 4x2 area, it would be useless for them to do so because they must terminate outside of it, which would be impossible.

The former two illustrations are examples of stranded colors and the latter is an example of a stranded region. We can detect both using connected component labeling. We start by assigning each continuous region of free space a unique identifier, which can be done efficiently via a disjoint-set data structure. Here are the results for the two states above (color hatching corresponds to region labels):

To see which colors and regions might be stranded, we keep track of which current positions and which goal dots are horizontally or vertically adjacent to each region. Then the logic is:

• For each non-completed color, there must exist a region which touches both its current position and goal position, otherwise the color is stranded.

• For each distinct region, there must exist some color whose current position and goal position touch it, otherwise the region is stranded.

It’s important to consider the space/time tradeoff presented by validity checks like these. Even though connected component analysis is pretty fast, it’s many orders of magnitude slower than just checking if a move is permitted; hence, adding a validity check will only provide an overall program speedup if performing it is faster on average than expanding all successors of a given node. On the other hand, these types of validity checks pretty much always reduce the space needed for search, because successors of states found to be unsolvable will never be allocated.

Chokepoint detection

Let us define a bottleneck as a narrow region of freespace of a given width \(W\). If closing the bottleneck renders more than \(W\) colors unsolvable (by separating their current and goal positions into distinct regions of freespace), then the bottleneck has become a chokepoint, and the puzzle can not be solved. Here’s a example to help explain:

The cells cross-hatched in gray constitute a bottleneck separating the current and goal positions of red, blue, yellow, cyan, and magenta. No matter where any of those five flows go, they will have to pass through the shaded cells in order to reach their goals; however, since the bottleneck is just three cells wide, we have a chokepoint and the puzzle is unsolvable from this state.

Fast-forwarding

For this project, I chose to use a stack-based allocator to create nodes. Basically, a stack allocator is lovely when you want to be able to “undo” one or more memory allocations, and it dovetails perfectly with this search problem when it comes to handling forced moves.

Let’s say we discover, upon entering a particular state, that there is a forced move. Suppose the state resulting from the forced move passes all validity checks. If we enqueue this successor, we know it will be dequeued immediately. Why? Since forced moves cost zero, the cost-to-come has not increased, but the cost-to-go has decreased by one. Why go through all of the trouble to enqueue and dequeue it? Why not just skip the queue entirely?

Conversely, imagine that making the forced move leads to an unsolvable state. In this case, we might wish to “undo” the allocation of the successor node – after all, memory is limited, and we might want to use that slot of memory for a potentially-valid node later on!

But this approach doesn’t just work for a single forced move. What if one forced move leads to another and another, starting a chain of forced moves? Once again, we should skip the queue for all of the intermediate states, only enqueuing the final result state which has no forced moves, and which passes all of the validity checks. On the other hand, if at any point we fail a validity check after a forced move, then we can de-allocate the entire chain, saving lots of memory. Here’s an example of such a chain:

On the left, orange has just moved into the square adjacent to the cyan flow. Cyan must now follow the single-cell-wide passage until the flow is completed, creating a 2x1 stranded region that invalidates the entire chain; hence, we can de-allocate these two states along with all of the intermediate ones as well. For the purposes of memory usage, its as if none of these nodes ever existed.

Other whistles and bells

If a node is invalid, we would like it to fail a validity check as quickly as possible. Tests costs time, and we will often see a program speedup if we run the cheap ones first. Accordingly, my solver orders validity checks from fastest to slowest, starting with dead ends, then stranded regions/colors, and finally bottlenecks.

Viewed in this light, we can consider the dead-end check not just a way of verifying a node’s potential validity, but also as a test of whether we should allow the considerably more expensive connected component analysis code to execute at all. As a wise programmer observed, the fastest code is the code that never runs. Or by analogy to medicine, don’t schedule an MRI until after you’ve completed the physical examination!

There were a few other features which sped up puzzle solution, but which I won’t discuss in depth here. There is code to choose which dot of a pair should be a flow’s initial position and which one its goal; and other code to decide when to switch the active color. These little details can have a big impact on both runtime and memory use.

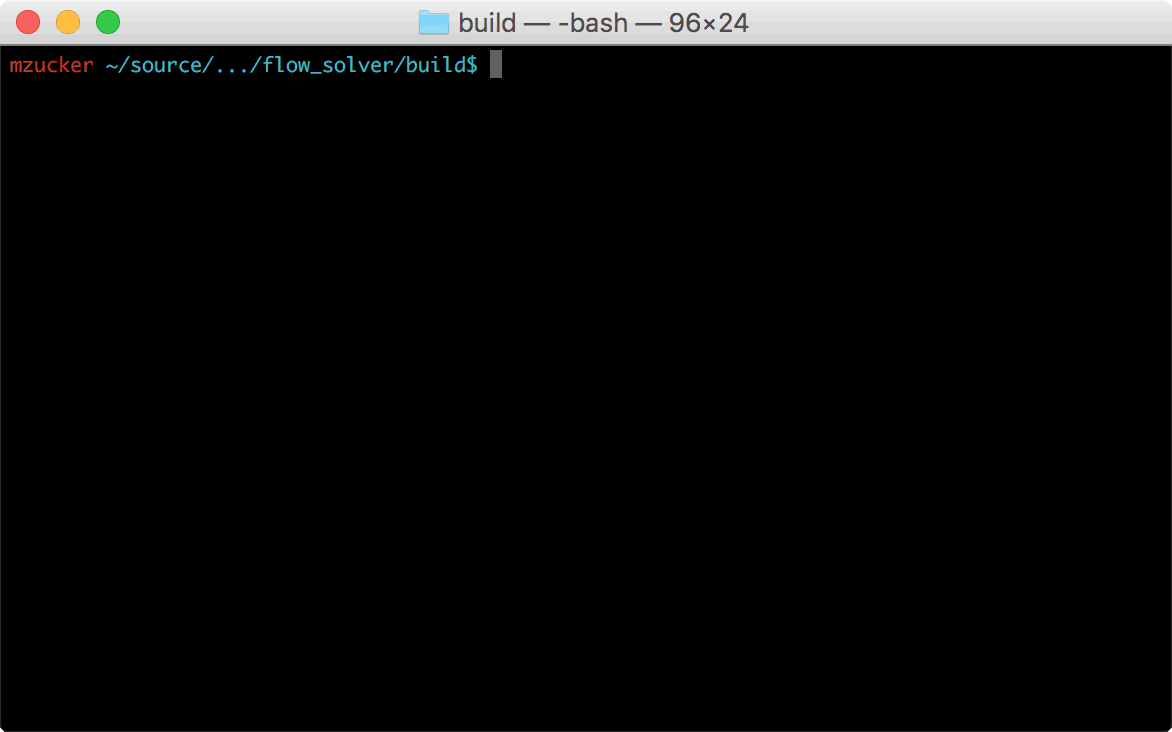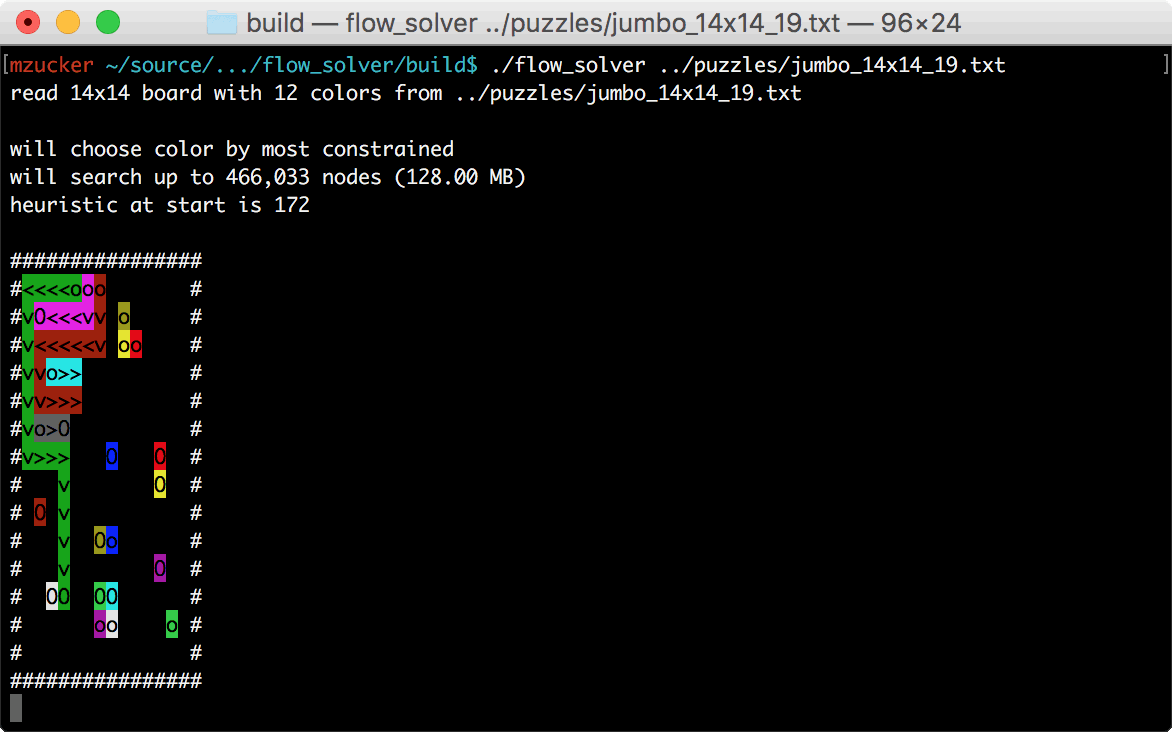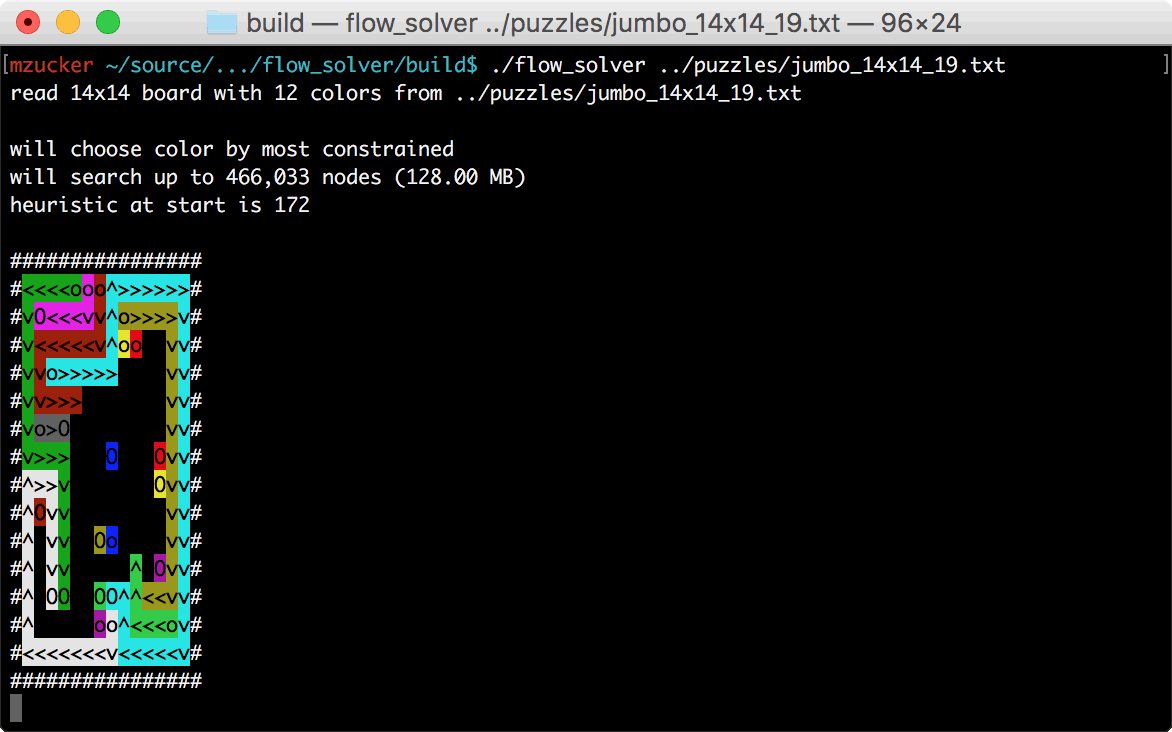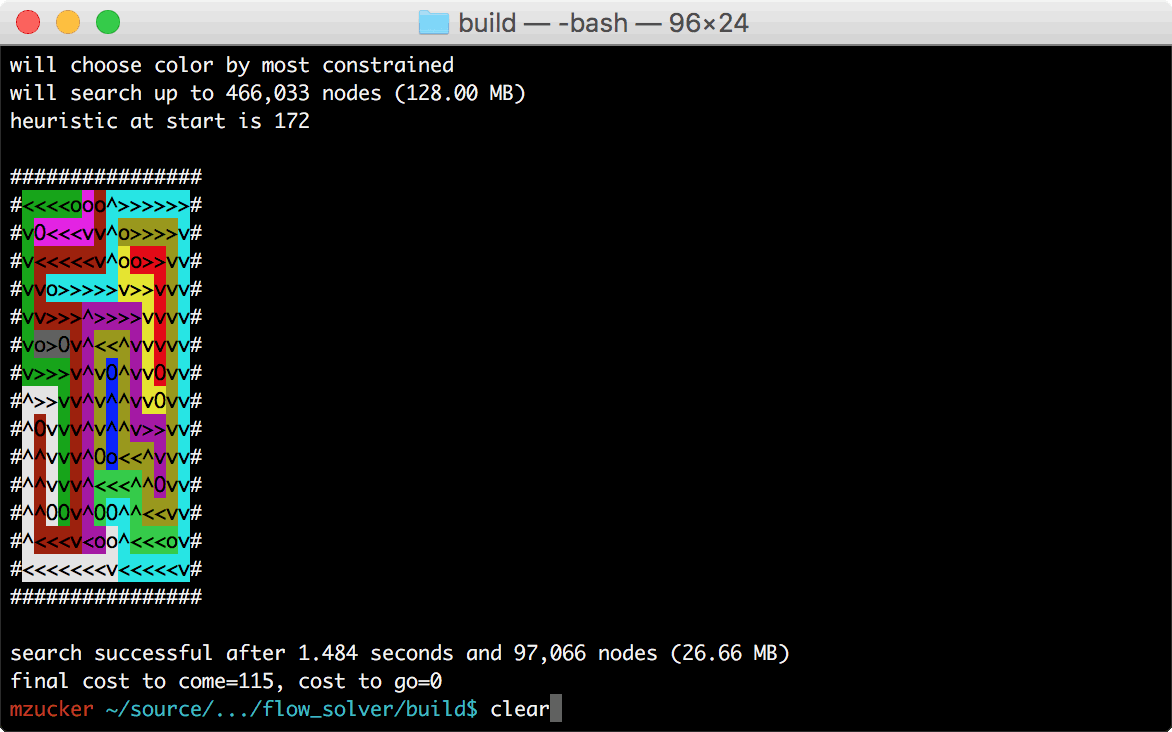
There’s also a way to load hints into the solver, which helped during development when I came across a puzzle that was taking too much space and time to solve. The jumbo_14x14_19.txt puzzle was the bane of my existence for a few days, but finally became tractable after I added a few more features. This site was helpful to check my work, too.

As I discovered in grad school, a good way to devise validity checks is to visualize intermediate states after a search has failed – if I can figure out how express in code the reasons why some of them are in fact invalid, I can prevent them from ever clogging up the tree in the first place.

Wrapping up

In the end, the program I wrote turned out a bit long and a bit complicated.¹ The good news is it that exposes just about every one of the features described above as a command-line switch – just run flow_solver --help to see them all.

Also, as I was preparing to write up this post, this happened on Facebook:

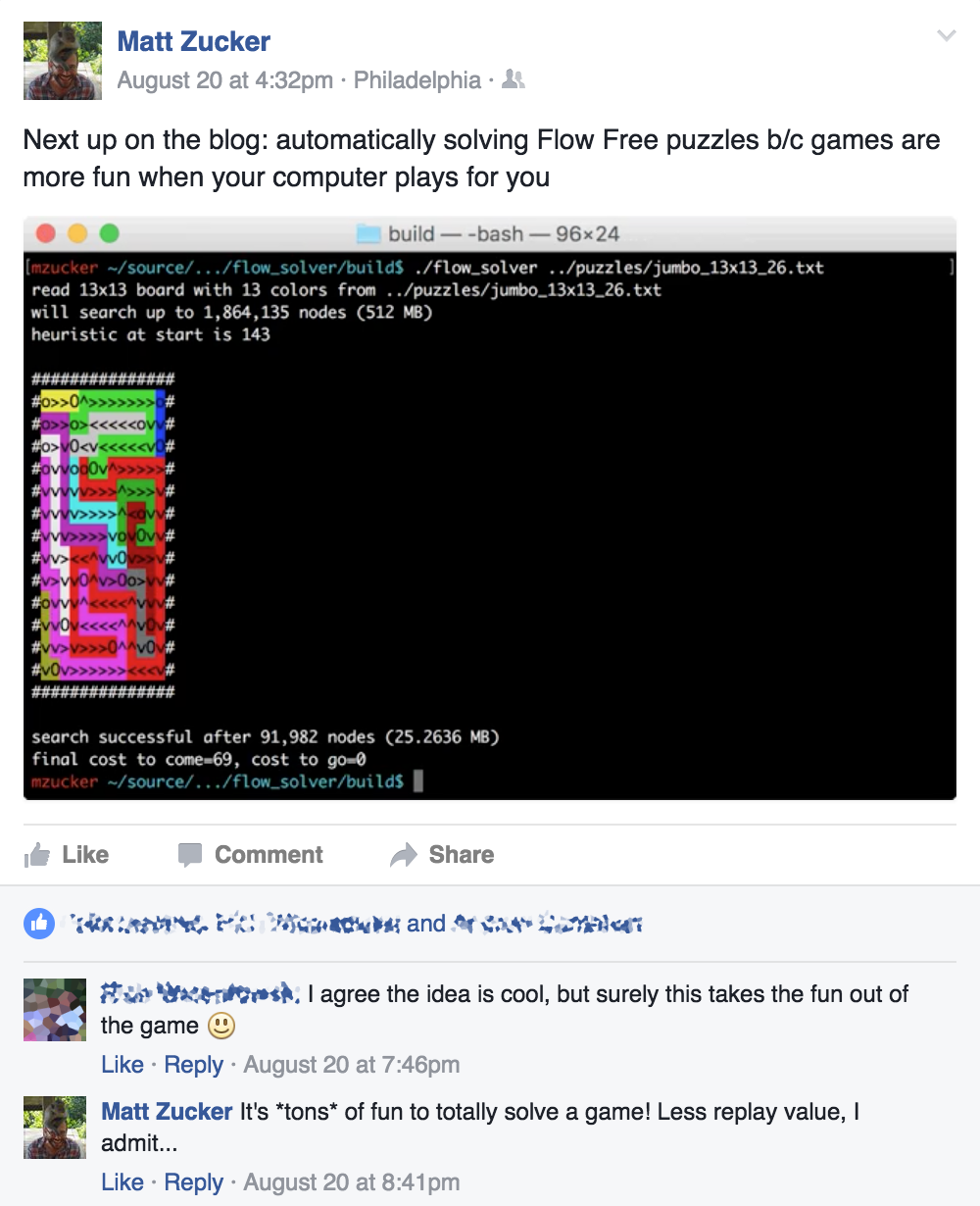
I want to say I was half-correct in my reply there – since I posted that last comment, I’ve gotten plenty of “replay value” out of trying to get the program to solve puzzles faster and better. So as a comparison, here’s a “scoreboard” of sorts showing the difference between the performance of the final program, and performance on August 21 – the day after this Facebook exchange – for all of the puzzles in the repository (lower is better in the “% of init” columns):

Puzzle	Init time	Final time	% of init	Init nodes	Final nodes	% of init
regular_5x5_01.txt	0.001	0.001	100%	16	16	100%
regular_6x6_01.txt	0.001	0.001	100%	26	25	96%
regular_7x7_01.txt	0.001	0.001	100%	42	40	95%
regular_8x8_01.txt	0.001	0.001	100%	64	55	86%
regular_9x9_01.txt	0.001	0.001	100%	206	166	81%
extreme_8x8_01.txt	0.001	0.001	100%	289	76	26%
extreme_9x9_01.txt	0.001	0.001	100%	178	111	62%
extreme_9x9_30.txt	0.002	0.001	100%	565	146	26%
extreme_10x10_01.txt	0.037	0.034	92%	7,003	4,625	66%
extreme_10x10_30.txt	0.024	0.008	33%	3,659	1,069	29%
extreme_11x11_07.txt	1.290	0.021	2%	197,173	2,645	1%
extreme_11x11_15.txt	0.103	0.004	4%	13,289	502	4%
extreme_11x11_20.txt	0.731	0.001	< 1%	102,535	227	< 1%
extreme_11x11_30.txt	0.167	0.003	2%	21,792	442	2%
extreme_12x12_01.txt	2.664	0.211	8%	315,600	20,440	6%
extreme_12x12_02.txt	0.052	0.013	25%	6,106	1,408	23%
extreme_12x12_28.txt	2.142	0.823	38%	283,589	84,276	30%
extreme_12x12_29.txt	0.657	0.107	16%	85,906	12,417	14%
extreme_12x12_30.txt	8.977	0.002	< 1%	1,116,520	330	< 1%
jumbo_10x10_01.txt	0.001	0.001	100%	235	167	71%
jumbo_11x11_01.txt	0.014	0.001	7%	1,627	210	13%
jumbo_12x12_30.txt	0.052	0.002	4%	6,646	345	5%
jumbo_13x13_26.txt	0.385	0.149	39%	38,924	16,897	43%
jumbo_14x14_01.txt	0.015	0.003	20%	1,399	389	28%
jumbo_14x14_02.txt	254.903	0.886	< 1%	20,146,761	61,444	< 1%
jumbo_14x14_19.txt	300.415	1.238	< 1%	29,826,161	97,066	< 1%
jumbo_14x14_21.txt	16.184	0.018	< 1%	1,431,364	1,380	< 1%
jumbo_14x14_30.txt	50.818	1.558	3%	4,577,817	130,734	3%

Note that I allowed the initial version of the program to use up to 8 GB of RAM, and still ran out of memory solving jumbo_14x14_19.txt (as mentioned above, it was a thorny one). Other fun observations:

• The final version is always at least as efficient as the initial, in terms of both time and space.

• The average improvement (speedup/reduction in storage) from initial to final was over 10x!

• The final version solves each puzzle in under 1.6 seconds, using less than 140K nodes.

Am I happy with the final results? Definitely. Did I waste waaay too much time on this project? For sure. Did my fiancée start binge-watching Stranger Things on Netflix without me while I was obsessing over Flow Free? Sadly, yes.

As usual, download the code yourself from github and give it a spin!

Appendix: Prior work

It turns out that I am unwittingly following in a long line of would-be Flow Free automators. Since I was in the air above southeast Asia when I started this project, I didn’t Google any of this, but now that I’m in documentation mode, here’s a chronological listing of what I could dig up:

• Jun 2011: just a video of a solver proceeding at a leisurely pace, couldn’t find source.
• Nov 2011: solver in C++ for a related puzzle, looks like a standard recursive backtracker.
• Aug 2012: solver in Perl, mothballed, doesn’t work, but README has a link to an interesting paper.
• Oct 2012: solver in C#, appears not to work based upon final commit message.
• Feb 2013: chatting about designing solvers in a C++ forum.
• Jul 2013: solver in R, framed as integer programming.²
• Sep 2013: two solvers from the same programmer, both in C#, both use DLX; author notes long solve times for large grids.
• Feb 2014: solver as coding assignment in a C++ class, yikes.
• Mar 2014: StackOverflow chat on designing a solver, top answer suggests reducing to SAT.³
• Feb 2016: solver in MATLAB using backtracking; very slow on puzzles >10x10 but it does live image capture and there’s a cool YouTube demo.

Without running the solvers listed here, it’s difficult to compare my performance to theirs, but I’d be willing to hazard an educated guess that mine is pretty speedy compared to the others, especially on large puzzles.

Comments

Comments are closed, see here for details.

richwiss · 2016-Aug-29

As someone who enjoys similar short interludes of FreeFlow, I have four questions. (Note that I skimmed bits of the code but there's no chance I understand it yet.)

1. In the two figures you have in the fast-forwarding section, you say "Cyan must now follow the single-cell-wide passage until the flow is completed, creating a 2x1 stranded region that invalidates the entire chain". I guess you are assuming that once a flow is next to the endpoint, you must flow to the endpoint, which makes ending a flow a zero-cost move. However, it would also be possible to go up (rather than right and ending the flow), then right, then down. This would have filled the 2x1 region that was leftover in your solution. There have been countless FreeFlow puzzles where I've filled otherwise stranded regions in order to solve the puzzle. What I don't know is if my solution at the time was simply an alternative way to solve it or if in fact that was the intended way to solve it. If it is the latter, that causes problems for your solver. For example, there is no found solution to this puzzle:

O.OG.
Y..YG
B.BR.
...R.
.....

The solution is

OoOGg
YyyYG
BbBR0
789R1
65432

where lowercase represents the flow and the numbers represent the path of the red flow.

2. There are many - perhaps a majority of? - FreeFlow puzzles that can be solved according to the "stay along the wall" algorithm where you first complete a flow that can be completed by staying along a wall (which creates a new wall), and then recursing until a solution is reached. Did you consider any speedup hacks of that nature while you were working on this?

3. Along the lines of #2, FreeFlow would consider your solutions "imperfect" because you didn't complete a single flow before moving on to the next. My hunch is that with the smaller puzzles you'd be able to solve these without too much of a performance impact. Any ideas? (Not sure where to hack at your code to enforce this but will look further.)

4. Your last few posts have been in Python. What made C a better choice? Previous infrastructure?

Matt Zucker · 2016-Aug-29

1. Pretty sure that up-right-down would violate the constraint that a colored flow cell has only two neighbors of the same color. I don't think Flow Free allows "looping back" like that.

2. Yep -- that's a big part of how I order things. Always start along the wall, prefer colors closer to wall (all else being equal), prefer most constrained move first. Tried hard to bring in some of that conventional wisdom.

3. Yes, big performance impact for larger puzzles. The code was doing this for a while but I disabled it because it helped solve tricky 14x14 ones. The good news is, you can always observe the solution the program produces and then enter it into the puzzle "the right way".

4. Speed! Also, I like using different languages for different tasks. A lot of the low-level operations in this program use bitwise operators -- for instance, we can track which flows have been completed with a 16-bit field, because there are a maximum of 16 colors. I would never have written the raytracer in Python, nor would I expect a solver like this to be nearly as fast in an interpreted language (but I'm sure someone will come along with JS and prove me wrong).

richwiss · 2016-Aug-29

1. Flow Free 11x11 Mania board 12 and my "perfect" solution are attached. And a link to a preferred solution: https://flowfreesolutions.com/...

2. Excellent.

3. Yes, of course you can redo them. I used to care about such things and take screenshots of my imperfect solutions so I could redo them. Browsing my screenshots found the solution attached below in March 2015. I no longer care :)

4. I promise never to write it in JS. Or Perl.

Matt Zucker · 2016-Aug-29

Ok, commit e44f007 now lets you disable the path self-touch test to make dumb solutions :)

Here's one that corresponds to neither solution you showed me:

asmeurer · 2016-Aug-29

In my experience playing the game, every puzzle has an "elegant" solution that doesn't require self touching paths, but often when solving by hand you end up using it, because just finding a solution at all is already hard enough without finding the true "elegant" solution.

Of course, the puzzles in the game are designed that way, but I imagine if you generated puzzles randomly you could create puzzles that are only solvable with self touching paths (as a simple example, imagine a large puzzle board with only one color).

asmeurer · 2016-Aug-29

What's so bad about using SAT or ILP? Techniques like the ones you've used here focus on how to *solve* a problem. When using a SAT solver, the actual logic of solving is encoded once in the solver. You instead must focus on how to *represent* the problem. But the beauty of this is that you can build up abstractions (to be sure, solvers also often must be built around those abstractions to keep things efficient). One could potentially represent a puzzle like Flow Free in a very high level and natural way and have it "compile" to a solver.

Matt Zucker · 2016-Aug-29

Maybe it's just personal preference? My own experience with generic algorithms to solve SAT, ILP, exact cover, etc. is that a) I spend more time trying to represent my problem to the solver than I would otherwise spend coding it up from scratch, and b) it can be hard/inefficient to represent domain knowledge that helps reject partial solutions early (like the validity checks here), or prioritize partial solutions.

On the other hand, the "if you have a hammer, the whole world looks like a nail" thing is a bit on the nose for me. I just like using tools I know, and I have a lot of experience with finagling best-first search to do what I want.

Also, I'm curious -- who are the end users of "industrial-strength" SAT solvers or ILP solvers? What are some real-world problems they shine on?

asmeurer · 2016-Aug-29

"Personal preference" is a lot different from "everyone who uses SAT has made poor life choices". I think SAT and similar solvers have very powerful potential, and it's disappointing to see people just throw them out the window (and insult those who use them).

Representational issues are a problem because most SAT solvers require input in CNF. I personally would like to see more solvers that allow representation in higher-level abstractions (Z3 has some great work in this area).

I agree that the domain knowledge thing is an issue. The best solution to that that I know of is to add pre-processing steps to trim the solution space.

My personal usage of SAT solvers is in the package dependency solver in conda. Basically, instead of representing package dependencies as a graph and trying to write a bunch of graph algorithms, you just represent dependencies as SAT (they translate quite nicely), and let the SAT solver figure it out. There's a bit more complexity once you turn it into an optimization problem (generally it's not enough to install a satisfiable set of packages, but rather a satisfiable set of packages with the newest versions), but it's still, in my opinion, nicer than writing the algorithms by hand. For instance, if you want to tweak the way the optimization works, it's just a matter of modifying a formula. Everything else in the code stays the same.

I know that in industry solvers are used for solving problems in operations research, and chip design (I don't have expertise in either of these, so I can't really say much more about them unfortunately).

Matt Zucker · 2016-Aug-31

https://twitter.com/matt_zucke...
Mea culpa

Michel Steiner · 2016-Nov-07

I also decided to try writing a Flow Free solver sometimes ago. Then I discovered your
interesting blog on the subject so I changed my goal… I’m now trying to write a
solver faster than yours! ;-)

After a lot of work, I’m now at <0.25 seconds worst time for the most complex 14x14
puzzle.

No A* search, no SAT, no heuristic! But quite a few lines of code to analyze the
board before starting (to remove some directions for some cells). Then I explore
the tree and attempt to find bad moves as soon as possible.

But I’m not sure we can compare directly our results… we are not using the same PC!

Also, I’m wondering if we are testing with the same set of puzzles!? Apparently you have
30 * 14x14. I found 90 of them, and I’m applying 8 different symmetries to each
puzzle to make sure the algorithm is not too sensible to the orientation of the
puzzle.

Do you think the run time with your 2 solutions is impacted by the orientation of the
puzzle? For example if you apply a rotation of 90, 180 or 270 degrees, or a
horizontal central symmetry, or both. Would your code continue to explore the
same number of nodes? (I can provide files with puzzle definitions if you are
interested).

Btw, have you seen puzzles larger than 14x14? I did not, and I’m wondering how well these
algorithms scale up!?

Matt Zucker · 2016-Nov-07

Glad I inspired you to try to beat me :) I don't have your code, but feel free to compare your code to mine on your PC, or open-source your solver so others can compare.

To be honest, I only have tested on the small number of 14x14 puzzles included in my github repository (see https://github.com/mzucker/flo... ). There are a large number of puzzles available at https://flowfreesolutions.com/... but they are only presented graphically, not in text form. I have no desire to hand-enter all of their posted puzzles, but you may be more enterprising than I am. I was also a bit concerned about fair use if I copied the entirety of the puzzle data set from another source and open-sourced it.

Almost certainly my C-based solver is sensitive to rotations/flips. I tried to make it less sensitive by assigning priorities based on distances from walls/center, but I imagine it would depend partially on the order the puzzle is defined in.

I have not tried any puzzles larger than 14x14, nor have I seen any out there. I'm pretty sure this problem is in NP (since both solution techniques I used are typically used for NP-hard problems); however, there are lots of problems ostensibly in NP that scale better than you might think on any real-world examples. This in fact was part of my initial, unfounded skepticism about SAT. The best answer seems to just be "try and see".

To be honest, I lost interest in optimizing my C solver when I realized my worst-case times were in the same ballpark as SAT. It seems silly to hand-tune a solution that encodes lots of domain knowledge when it's within less than an order of magnitude of a turn-key, "know nothing" solution.

Michel Steiner · 2016-Nov-08

My code is not clean enough to be published as open source (at least not yet - I’m not a professional developer). But of course I’m ready to email it to you if you’re interested. Potential problem… it’s written in VB.NET (nobody’s perfect! ;-)). I’m not a C specialist and did not manage to run your code. Is it supposed to run under Windows/Visual Studio?

I also have a limited number of puzzles. I managed to extract their definitions from files I found after installing Flow Free on a device! I found 2’490 puzzles ranging from 5x5 to
14x14 (90 of them are 14x14). Multiply these number by 8 with the possible symmetries. There are more puzzles available (for example there is a pack with 150 * 14x14), but I did not find their definition files. Good point about “fair use of these puzzles”. We have to be careful about this…

I understand your last point about SAT which is more generic. But my point is that if you had added a few more optimizations into your C solver, it would have decreased the number of nodes to explore by a very large amount. For example you explore 130’734 nodes for the 14x14_30 puzzle, while my solver only explores 274 nodes for that problem (with run time of 3ms). Some of these optimizations only require a few lines of code and have profound effects. I think this re-opens the question "is SAT better than A* Search" for this problem?

Note that my solver only searches for “elegant” solutions with no self-touching path (as explained by asmeurer). In fact, it helps doing this because it decreases the number of possibilities to explore. Not sure what’s your latest code do?

Btw, I added a new powerful optimization this morning. New worst case: 63ms (5’758 nodes to explore). It’s with a puzzle you did not try. I have tried a few additional optimisations, but sometimes the cost of running them it too high for the benefit they bring.

Just curious, is the SAT solution sensible to rotations/symmetries? And is there a way to make it more efficient?

Matt Zucker · 2016-Nov-08

Michel - you raise a lot of interesting points, sounds like you're almost ready to start your own blog!

Michel Steiner · 2016-Nov-10

Oh, I’m sorry! I thought it was appropriate to discuss the subject on your blog.

I won’t create my own blog, but I’ll continue improving the code. The more I think
about it, the more I find ways to make things faster. It seems to me that the
key to write a fast solver is to find forced and bad moves rapidly. The
algorithm to traverse the tree is not that important after all, because there
is not that many nodes to explore! Did you say needlessly complex? ;-)

Michel Steiner · 2017-Jan-17

Matt – I’ve a file with the definition for 150 * 15x15 puzzles, if you’re interested to test your solutions with larger puzzles.

1. Please consult blog title if surprised. ↩

2. In my limited experience, if you have to solve a problem and the best way you can express it is as an integer program, you have made poor life choices. ↩

3. Same. If your best choice for a problem is “reduce to SAT”, maybe find a new problem? ↩