The Perlin noise math FAQ

by Matt Zucker

v. 1.0, last updated February 2001

Disclaimer, January 2017: This document is glaringly outdated (note last update above) and is presented primarily for historical interest, because other archived copies have begun to disappear/bit rot. While I'm not aware of are any glaring inaccuracies, it's certainly not the document I would write now if I wanted to present a modern tutorial on procedural noise for graphics.

Turns out that 20-year-old me was missing a few key concepts, for instance the relationship between the "ease curve" discussed below and the cubic hermite spline that underlies the GLSL smoothstep function.

Many of the links below are broken, follow at your own risk.

If you're interested in a more modern take on these topics, a great place to start would be Inigo Quilez's articles and shadertoy examples.

Table of Contents

About this document

So far, I have found two really great sources for information about Perlin noise. They are Ken Perlin's Making Noise web site, which has a comprehensive introduction to the topic, and Hugo Elias's page, which features some algorithms and a few more detailed examples of applications. This document is intended to complement those two valuable resources by explaining in more depth, hopefully in plain English, some of the math involved in Ken Perlin's original implementation of Perlin noise.

I wrote a demo program in C++ that includes a Perlin noise texture class, which I hope provides a decent example of C++ code for Perlin noise. You can find the demo at http://www.robo-murito.net/code.html.

What is Perlin noise?

Perlin noise is function for generating coherent noise over a space. Coherent noise means that for any two points in the space, the value of the noise function changes smoothly as you move from one point to the other -- that is, there are no discontinuities.


Non-coherent noise (left) and Perlin noise (right)

When I talk about a noise function, I mean a function that takes a coordinate in some space and maps it to a real number between -1 and 1. Note that you can make noise functions for any arbitrary dimension. The noise functions above are 2-dimensional, but you can graph a 1-dimensional noise function just like you would graph any old function of one variable, or consider noise functions returning a real number for every point in a 3D space.

These images were all created using nothing but Perlin noise:

Besides these trivial images, there are countless interesting applications for noise in computer graphics. Look at Hugo Elias' page or Ken Perlin's pages for some pretty examples, in-depth explanations and nifty ideas.

How do you generate Perlin noise?

I've seen implementations on the internet that take non-coherent noise, as shown above, and smooth it (with something like a blur function) so it becomes coherent noise, but that can end up being more computationally expensive than the function I'll present here, which is more or less the original implementation that Ken Perlin came up with. The problem with Perlin's implementation on its own was that that reading the descriptions of the math published on Perlin's website was a bit like reading Greek -- it took me about a week of reading his code and notes to figure out the actual geometric interpretations of the math. So hopefully this document can trim down that learning curve.

Let's look at the 2D case, where we have the function

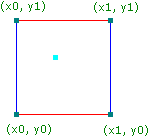
noise2d(x, y) = z,
with x, y, and z all real (floating-point) numbers. We'll define the noise function on a regular grid, where grid points are defined for each whole number, and any number with a fractional part (i.e. 3.14) lies between grid points. Consider finding the value of noise2d(x, y), with x and y both not whole numbers -- that is, the point (x, y) lies somewhere in the middle of a square in our grid. The first thing we do is look at the gridpoints surrounding (x, y). In the 2D plane, we have 4 of them, which we will call (x0, y0), (x0, y1), (x1, y0), and (x1, y1).


The 4 grid points bounding (x, y)

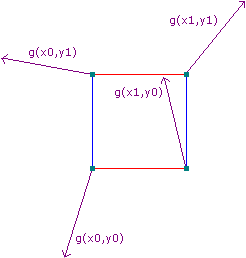
Now we need a function

g(xgrid, ygrid) = (gx, gy)
which takes each grid point and assigns it a pseudorandom gradient of length 1 in R2 ('gradient' is just the name for an ordered pair or vector that we think of as pointing in a particular direction). By pseudorandom, we mean that g has the appearance of randomness, but with the important consideration that it always returns the same gradient for the same grid point, every time it's calculated. It's also important that every direction has an equal chance of being picked.


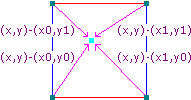
The 4 pseudorandom gradients associated with the grid points

Also, for each grid point, we generate a vector going from the grid point to (x, y), which is easily calculated by subtracting the grid point from (x, y).


Vectors from the grid points to (x, y)

Now we have enough to start calculating the value of the noise function at (x, y). What we'll do is calculate the influence of each pseudorandom gradient on the final output, and generate our output as a weighted average of those influences.

First of all, the influence of each gradient can be calculated by performing a dot product of the gradient and the vector going from its associated grid point to (x, y). A refresher on the dot product -- remember, it's just the sum of the products of all the components of two vectors, as in

(a, b) · (c, d) = ac + bd .
Since I'm really tired of writing subscripts, we'll just refer to these 4 values as s, t, u, and v, where
s = g(x0, y0) · ((x, y) - (x0, y0)) ,
t = g(x1, y0) · ((x, y) - (x1, y0)) ,
u = g(x0, y1) · ((x, y) - (x0, y1)) ,
v = g(x1, y1) · ((x, y) - (x1, y1)) .
So here's a 3D-ish picture of some influences s, t, u, and v coming out of the R2 plane (note that these probably wouldn't be the actual values generated by the dot products of the vectors pictured above).


Influences from the grid points

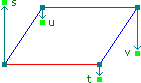
Geometrically, the dot product is proportional to the cosine of the angle between two vectors, though its unclear to me if that geometrical interpretation helps one visualize what's going on. The important thing to know at this point is that we have four numbers, s, t, u, and v which are uniquely determined by (x, y) and the pseudorandom gradient function g. Now we need a way to combine them to get noise2d(x, y), and as I suggested before, some sort of average will do the trick.

I'm going to state the obvious here and say that if we want to take an average of four numbers, what we can actually do is this:

  1. find the average of the first pair of numbers
  2. find the average of the second pair of numbers
  3. average those two new numbers together
-- and that's the strategy we'll take here. We'll average the "front" values s and t first, then average the "rear" values u and v. This works to our advantage because the points below s and t, and similarly below u and v vary only in the x dimension -- so we only have to worry about dealing with one dimension at a time.

We're not taking a plain vanilla-flavored average here, but instead, a weighted average. That is, the value of the noise function should be influenced more by s than t when x is closer to x0 than x1 (as is the case in the pictures above). In fact, it ends up being nice to arrange things so that x and y values behave as if they are slightly closer to one grid point or the other than they actually are because that has a smoothing effect on the final output. I know that sounds really silly, but noise without this property looks really stupid. In fact, it sounds so silly that I'm going to write it again: we're going to want the input point to behave as if its closer to one grid point or another than it actually is.

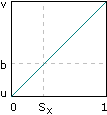
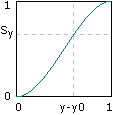
This is where we introduce the concept of the ease curve. The function 3p² - 2p³ generates a nice S-shaped curve that has a few characteristics that are good for our purposes.


Meet the ease curve

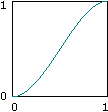
What the ease curve does is to exaggerate the proximity its input to zero or one. For inputs that are sort of close to zero, it outputs a number really close to zero. For inputs close to one, it outputs a number really close to one. And when the input is exactly one half, it outputs exactly one half. Also, it's symmetrical in the sense that it exaggerates to the same degree on both sides of p = ½. So if we can treat one grid point as the zero value, and the other as the one value, the ease curve has the exact smoothing effect that just we said we wanted.

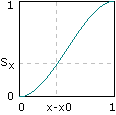
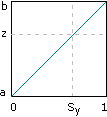
Ok, I've droned on long enough, it's calculation time: first, we take the value of the ease curve at x - x0 to get a weight Sx. Then we can find the weighted average of s and t by constructing a linear function that maps 0 to s and 1 to t, and evaluating it at our x dimension weight Sx. We'll call this average a. We'll do the same for u and v, and call the result b.


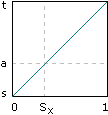
Finding the first two averages using linear interpolation

The above figures should satisfy you that no matter where x happens to fall in the grid, the final averages will always be between s and t, and u and v, respectively. Mathematically, this is all simple to calculate:

Sx = 3(x - x0)² - 2(x - x0)³
a = s + Sx(t - s)
b = u + Sx(v - u)
Now we find our y dimension weight, Sy, by evaluating the ease curve at y - y0, and finally we take a weighted sum of a and b to get our final output value z.


A weighted sum of the first two averages yields the final output

And there you have it. So all you have to do is call the noise function for every pixel you want to color, and you're done. Probably.

...and they all lived happpily ever after.

The End.

An interesting consequence of all of this is that the noise function becomes zero when x and y are both whole numbers. This is because the vector (x, y) - (x0, y0) will be the zero vector. Then the dot product of that vector and g(x0, y0)will evaluate to zero, and the weights for the averages will also always be zero, so that the zero dot product will influence the final answer 100%. The funny thing is that looking at the noise function, you would never guess that it ends up being zero at regular intervals.

Computational complexity

If you want to extend the noise function to n dimensions, you'll need to consider 2n grid points, and perform 2(n - 1) weighted sums. The implementation presented here has a computational complexity of O(2(n - 1)), which means that you'll really start to drag if you want to look at 5-, 6-, or greater dimensional noises.

Speeding it up

We could increase the speed of the noise function if we didn't have to compute the pseudorandom gradient every time we called the noise function (because for every x between some x0 and x1 and y between some y0 and y1, we have to recalculate the same four gradients every time the noise function is called!) The nice thing to do would be to precalculate the gradient for every possible (xgrid, ygrid), but xgrid and ygrid are allowed to vary all over the real plane! How could we possible precalculate every value?

The neat thing about noise is that it's locally variable, but globally flat -- so if we zoom out to a large degree, it will just look like a uniform value (zero in fact). So, we don't care if the noise function starts to repeat after large intervals, because once you're zoomed out far enough to see the repeat, it all looks totally flat anyways.

So now we should feel justified in doing a little trick with modulus. Say we're doing noise in 3D, and we want to find the gradient for some grid point (i, j, k). Let's precompute a permutation table P, that maps every integer from 0 to 255 to another integer in the same range (possibly even the same number). Also, let's precompute a table of 256 pseudorandom gradients and put it in G, so that G[n] is some 3-element gradient.

Now,

g(i, j, k) = G[ ( i + P[ (j + P[k]) mod 256 ] ) mod 256 ]
But on a computer, modulus with 256 is the same thing as a bitwise and with 255, which is a very fast operation to perform. Now we've reduced the problem of a possibly involved function call into nothing but some table lookups and bitwise operations. Granted, the gradients repeat every 256 units in each dimenstion, but as demonstrated, it doesn't matter.

This speedup is also mentioned on Perlin's web page, and is actually used in his original implementation.

Looping noise

What if you want to use procedural noise to calculate a repeating animation of a licking flame or rolling clouds? It is true that noise on it's own doesn't tend to repeat discernably, and that's great for generating ever-changing images; however, if you want to prerender an animation, you'll probably want it to repeat. Given that F is your function that generates a real number from a point in noise-space, and you want your animation to repeat every t units, you define a new function that loops when z is between 0 and t:
Floop(x, y, z) = ( (t - z) * F(x, y, z) + (z) * F(x, y, z - t) ) / (t)
Now each function call takes twice as long to calculate, but since you're probably not going to use this cycling technique in real time, it probably doesn't matter.

The explanation

Consider the graph of a noise function F(x, y, z) for some fixed x and y. The problem is, you want F(0) = F(t) and there is no guarantee that will be the case with any old x, y, and t. Actually, since any given x and y should have no influence on the repeating aspect of the animation, we can for all practical purposes throw them out while we're developing our repeating function, and consider the simplified case of a one-dimensional noise function F(z).


A one-dimensional noise function

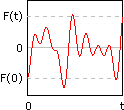
We need to take this function and change it into one where it is guaranteed that F(0) = F(t). Here's an expanded view of our noise function showing its behavior from -t to t:


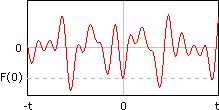
The same, function, ranging over a positive and negative domain

Now we define a new function F'(z) that behaves like F(z) when z is near zero, but behaves like F(z - t) when z is near t. If you think about it, you see that F'(0) = F(0), and that F'(t) = F(t - t) = F(0). We can do this with a simple linear interpolation by considering a linear function which is equal to F(z) at 0, and equal to F(z - t) at t.

High school algebra tells us that this linear function has a slope of

(rise) / (run) = (F(z - t) - F(z)) / (t - 0) = (F(z - t) - F(z)) / t
and an intercept of F(z). Now we set up F' as this linear interpolation operating on z:
F'(z) = slope(z) + intercept
        = ( (F(z - t) - F(z)) / t )(z) + F(z)
        = ( ( (z) * F(z - t) - (z) * F(z) ) / t ) + F(z)
        = ( ( (z) * F(z - t) - (z) * F(z) ) / t ) + (t / t) * F(z)
        = ( (z) * F(z - t) - (z) * F(z) + (t) * F(z)) / (t)
        = ( (z) * F(z - t) + (t-z) * F(z) ) / (t)
        = ( (t-z) * F(z) + (z) * F(z - t) ) / (t)
Which is basically the same as the function given above. If you look at F' next to F, you can see that the function does indeed repeat in that F'(0) = F'(t). Also notice that the peaks just to the right of F'(0) are the same as the peaks just to the right of F'(0), and that the peaks just to the left of F'(t) are virtually identical to the peaks just to the left of F(0).


The old function (left), and the new, repeating function (right)

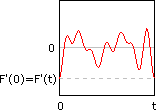
If you had a little calculus and too much free time, you could prove that this looping (and the tiling in the next section) is truly seamless: not only does F(0) = F'(t), but all their derivatives should match up as well. Which means that no one should be able to tell where the repeat actually happens.

Seamlessly tiling noise

Say you're using a noise function to generate textures for a polygon-based engine. Chances are, you might want the textures to be tileable. You can extend the above example to generate tileable 2-dimensional noise that repeats every w units in the x dimension and every h units in the y dimension. This will require a weighted sum of four calls to the original function (which again, for lack of imagination, we will call F).
Ftileable(x, y) = (
       F(x, y) * (w - x) * (h - y) +
       F(x - w, y) * (x) * (h - y) +
       F(x - w, y - h) * (x) * (y) +
       F(x, y - h) * (w - x) * (y)
) / (wh)
A pattern should be emerging here, so it shouldn't surprise you that you'll need evaluate a weighted sum of 8 calls to the noise function if you want to have a repeating animation that tiles in the x and y dimenstions. I'm not going to write it out here out of space considerations, and also because it should be evident what the sum will be.